Probability plots to check the goodness of fit of parametric models
probPlot.RdprobPlot provides four types of probability plots: P-P plot, Q-Q plot, Stabilised probability plot, and Empirically Rescaled plot to check if a certain distribution is an appropiate choice for the data.
# Default S3 method
probPlot(times, cens = rep(1, length(times)),
distr = c("exponential", "gumbel", "weibull", "normal",
"lognormal", "logistic", "loglogistic", "beta"),
plots = c("PP", "QQ", "SP", "ER"),
colour = c("green4", "deepskyblue4", "yellow3",
"mediumvioletred"), mtitle = TRUE, ggp = FALSE,
m = NULL, betaLimits = c(0, 1), igumb = c(10, 10),
prnt = FALSE, degs = 3,
params0 = list(shape = NULL, shape2 = NULL,
location = NULL, scale = NULL), print.AIC = TRUE,
print.BIC = TRUE, ...)
# S3 method for class 'formula'
probPlot(formula, data, ...)Arguments
- times
Numeric vector of times until the event of interest.
- cens
Status indicator (1, exact time; 0, right-censored time). If not provided, all times are assumed to be exact.
- distr
A string specifying the name of the distribution to be studied. The possible distributions are the exponential (
"exponential"), the Weibull ("weibull"), the Gumbel ("gumbel"), the normal ("normal"), the lognormal ("lognormal"), the logistic ("logistic"), the loglogistic ("loglogistic"), and the beta ("beta") distribution.- plots
Vector stating the plots to be displayed. Possible choices are the P-P plot (
"PP"), the Q-Q plot ("QQ"), the Stabilised Probability plot ("SP"), and the Empirically Rescaled plot ("ER"). By default, all four plots are displayed.- colour
Vector indicating the colours of the displayed plots. The vector will be recycled if its length is smaller than the number of plots to be displayed.
- mtitle
Logical to add or not the title "Probability plots for a
distrdistribution" to the plot. Default isTRUE.- ggp
Logical to use or not the ggplot2 package to draw the plots. Default is
FALSE.- m
Optional layout for the plots to be displayed.
- betaLimits
Two-components vector with the lower and upper bounds of the Beta distribution. This argument is only required, if the beta distribution is considered.
- igumb
Two-components vector with the initial values for the estimation of the Gumbel distribution parameters.
- prnt
Logical to indicate if the maximum likelihood estimates of the parameters should be printed. Default is
TRUE.- degs
Integer indicating the number of decimal places of the numeric results of the output.
- params0
List specifying the parameters of the theoretical distribution. By default, parameters are set to
NULLand estimated with the maximum likelihood method. This argument is only considered, if all parameters of the studied distribution are specified.- formula
A formula with a numeric vector as response (which assumes no censoring) or
Survobject.- data
Data frame for variables in
formula.- print.AIC
Logical to indicate if the AIC of the model should be printed. Default is
TRUE- print.BIC
Logical to indicate if the BIC of the model should be printed. Default is
TRUE- ...
Optional arguments for function
par, ifggp = FALSE.
Details
By default, function probPlot draws four plots: P-P plot,
SP plot, Q-Q plot, and EP plot. Following, a description is given for
each plot.
The Probability-Probability plot (P-P plot) depicts the empirical distribution, \(\widehat{F}(t)\), which is obtained with the Kaplan-Meier estimator if data are right-censored, versus the theoretical cumulative distribution function (cdf), \(\widehat{F_0}(t)\). If the data come from the chosen distribution, the points of the resulting graph are expected to lie on the identity line.
The Stabilised Probability plot (SP plot), proposed by Michael (1983), is a transformation of the P-P plot. It stabilises the variance of the plotted points. If \(F_0 = F\) and the parameters of \(F_0\) are known, \(\widehat{F_0}(t)\) corresponds to the cdf of a uniform order statistic, and the arcsin transformation stabilises its variance. If the data come from distribution \(F_0\), the SP plot will resemble the identity line.
The Quartile-Quartile plot (Q-Q plot) is similar to the P-P plot, but it represents the sample quantiles versus the theoretical ones, that is, it plots \(t\) versus \(\widehat{F}_0^{-1}(\widehat{F}(t))\). Hence, if \(F_0\) fits the data well, the resulting plot will resemble the identity line.
A drawback of the Q-Q plot is that the plotted points are not evenly spread. Waller and Turnbull (1992) proposed the Empirically Rescaled plot (EP plot), which plots \(\widehat{F}_u(t)\) against \(\widehat{F}_u(\widehat{F}_0^{-1}(\widehat{F}(t)))\), where \(\widehat{F}_u(t)\) is the empirical cdf of the points corresponding to the uncensored observations. Again, if \(\widehat{F}_0\) fits the data well, the ER plot will resemble the identity line.
By default, all four probability plots are drawn and the maximum
likelihood estimates of the parameters of the chosen parametric model
are returned. The parameter estimation is acomplished with the
fitdistcens function of the fitdistrplus package.
Value
If prnt = TRUE, the following output is returned:
DistributionDistribution under study.
ParametersParameters used to draw the plots (if
params0is provided).EstimatesA list with the maximum likelihood estimates of the parameters of all distributions considered.
StdErrorsVector containing the estimated standard errors.
aicThe Akaike information criterion.
bicThe so-called BIC or SBC (Schwarz Bayesian criterion).
In addition, a list with the same contents is returned invisibly.
References
J. R. Michael. The Stabilized Probability Plot. In: Biometrika 70 (1) (1983), 11-17. URL: https://doi.org/10.1093/biomet/70.1.11
L.A. Waller and B.W. Turnbull. Probability Plotting with Censored Data. In: American Statistician 46 (1) (1992), 5-12. URL: https://doi.org/10.1080/00031305.1992.10475837
Examples
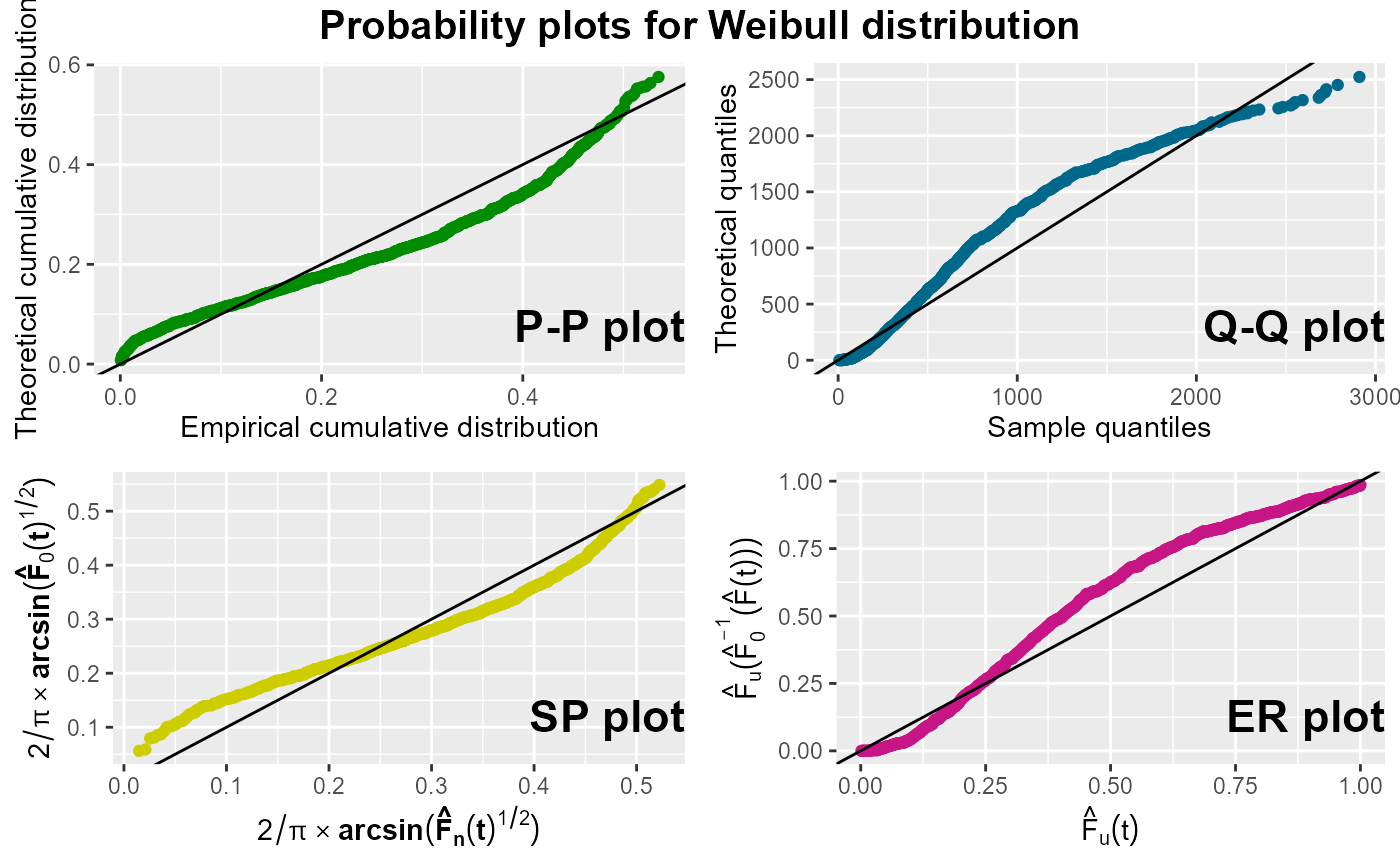
# P-P, Q-Q, SP, and EP plots for complete data
set.seed(123)
x <- rlnorm(1000, 3, 2)
probPlot(x)
 probPlot(x, distr = "lognormal")
probPlot(x, distr = "lognormal")
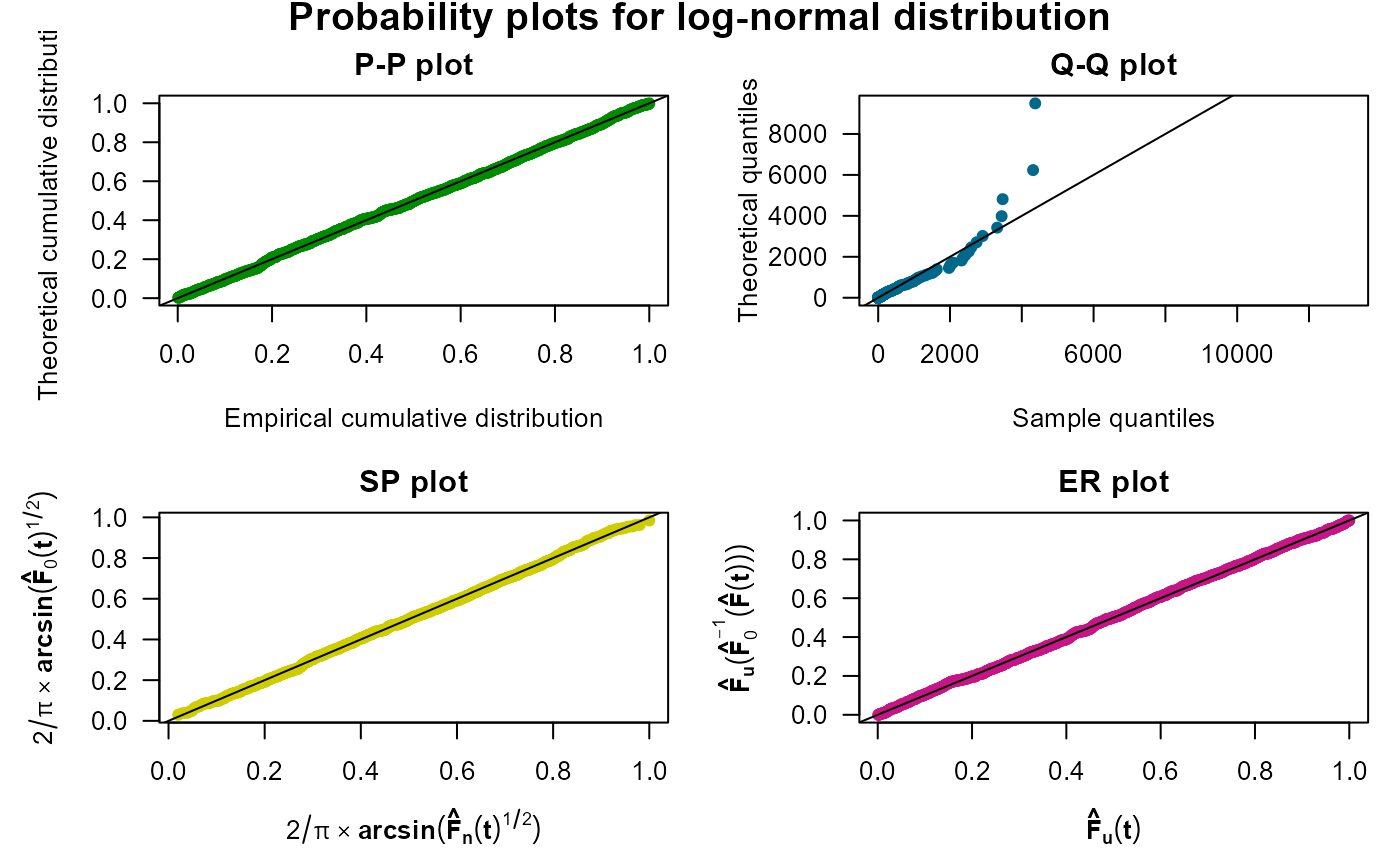 # P-P, Q-Q, SP, and EP plots for censored data using ggplot2
probPlot(Surv(time, status) ~ 1, colon, "weibull", ggp = TRUE)
# P-P, Q-Q, SP, and EP plots for censored data using ggplot2
probPlot(Surv(time, status) ~ 1, colon, "weibull", ggp = TRUE)
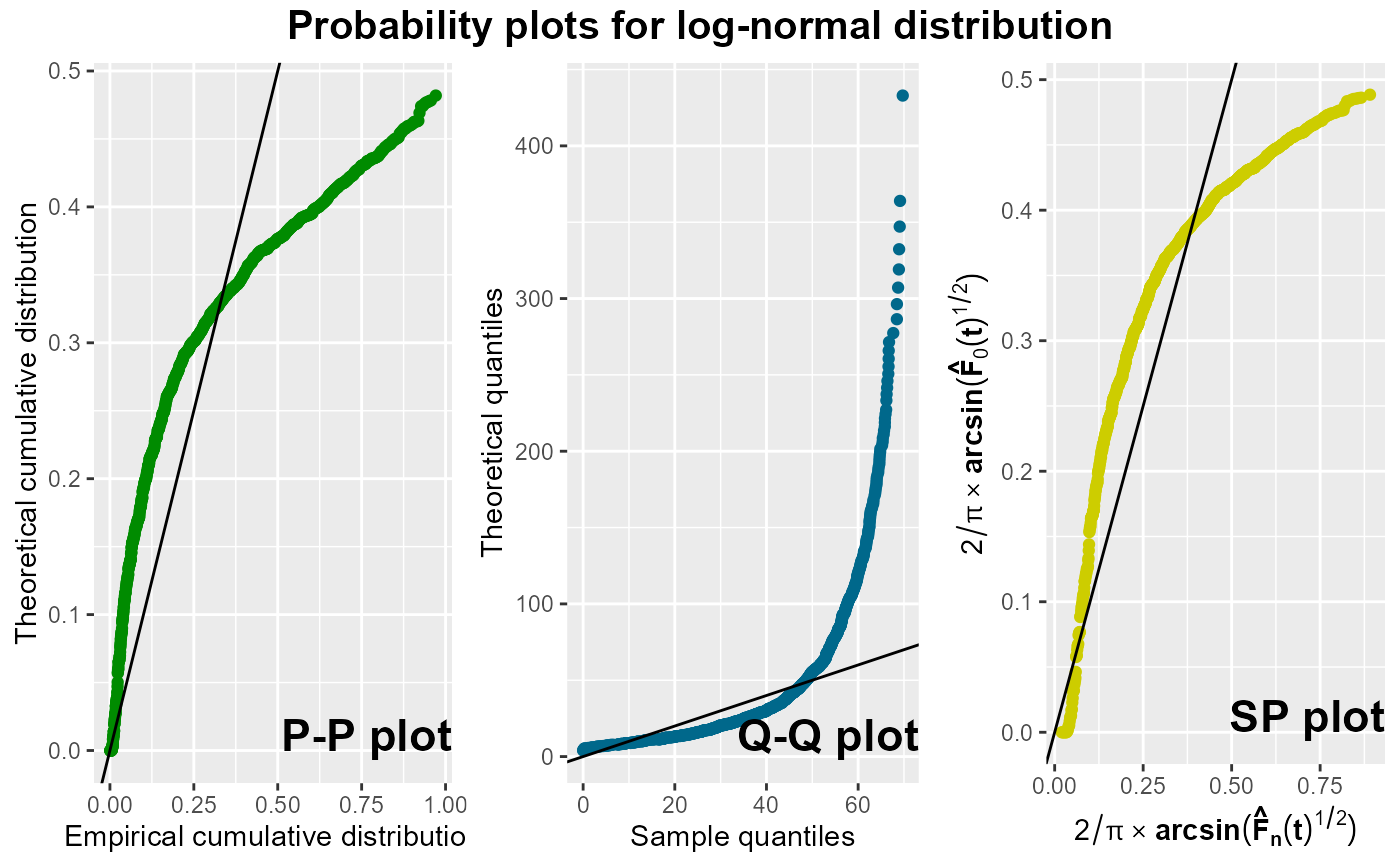
 # P-P, Q-Q and SP plots for censored data and lognormal distribution
data(nba)
probPlot(Surv(survtime, cens) ~ 1, nba, "lognorm", plots = c("PP", "QQ", "SP"),
ggp = TRUE, m = matrix(1:3, nr = 1))
# P-P, Q-Q and SP plots for censored data and lognormal distribution
data(nba)
probPlot(Surv(survtime, cens) ~ 1, nba, "lognorm", plots = c("PP", "QQ", "SP"),
ggp = TRUE, m = matrix(1:3, nr = 1))